Materi matematika grafik merupakan bagian penting dalam memahami visualisasi data. Melalui grafik, kita dapat dengan mudah melihat pola, tren, dan hubungan antar variabel dalam suatu data. Grafik dapat memberikan gambaran yang jelas dan cepat tentang informasi yang terkandung dalam data, sehingga memudahkan pemahaman dan analisis.
Materi ini akan membahas berbagai jenis grafik, mulai dari grafik fungsi linear, kuadrat, eksponensial, trigonometri, grafik bar, lingkaran, dan titik-titik. Kita juga akan mempelajari konsep koordinat kartesius, prinsip dasar menggambar grafik, dan penerapannya dalam kehidupan sehari-hari dan berbagai bidang ilmu. Selain itu, materi ini akan memberikan contoh soal dan latihan untuk memperdalam pemahaman.
Definisi Materi Matematika Grafik
Materi matematika grafik membahas representasi visual dari hubungan antar variabel. Grafik digunakan untuk mempermudah pemahaman pola dan tren dalam data, serta membantu dalam menganalisis dan memprediksi perilaku variabel tersebut.
Konsep Dasar Materi Grafik
Konsep dasar dalam materi grafik meliputi koordinat kartesius, yang digunakan untuk menentukan posisi titik pada bidang datar. Pemahaman tentang sumbu x dan sumbu y, serta bagaimana titik-titik diplot di atasnya, sangat penting. Selain itu, pemahaman tentang kemiringan (slope) dan titik potong (intercept) sangat membantu dalam menganalisis hubungan antar variabel yang diwakilkan dalam grafik.
Jenis-Jenis Grafik
Berbagai jenis grafik digunakan dalam matematika untuk mewakili data dan hubungan antar variabel. Masing-masing grafik memiliki kegunaan dan karakteristik yang berbeda, tergantung pada jenis data yang akan divisualisasikan.
- Grafik Koordinat Kartesius: Grafik yang paling umum digunakan, menggunakan sumbu x dan y untuk menentukan posisi titik.
- Grafik Fungsi: Grafik yang menggambarkan hubungan antara variabel x dan y, di mana setiap nilai x memiliki satu nilai y yang sesuai.
- Grafik Bar: Grafik yang menggunakan batang untuk membandingkan nilai antar kategori.
- Grafik Lingkaran (Pie Chart): Grafik yang menggunakan potongan lingkaran untuk menunjukkan proporsi dari keseluruhan.
- Grafik Garis: Grafik yang menggunakan garis untuk menunjukkan tren dan perubahan nilai variabel dari waktu ke waktu.
- Grafik Titik-Titik (Scatter Plot): Grafik yang menunjukkan hubungan antara dua variabel dengan memplot titik-titik pada bidang koordinat.
Perbandingan Jenis Grafik
| Jenis Grafik | Kegunaan | Kelebihan | Kekurangan |
|---|---|---|---|
| Grafik Bar | Membandingkan nilai antar kategori | Mudah dipahami, visualisasi data kategorikal yang jelas | Kurang efektif untuk menunjukkan tren atau perubahan kontinu |
| Grafik Lingkaran | Menunjukkan proporsi dari keseluruhan | Menunjukkan proporsi dengan jelas | Sulit untuk membandingkan lebih dari beberapa kategori |
| Grafik Garis | Menunjukkan tren dan perubahan nilai dari waktu ke waktu | Memvisualisasikan perubahan kontinu dengan baik | Data diskrit mungkin kurang efektif |
Contoh Grafik Fungsi Kuadrat
Fungsi kuadrat memiliki bentuk umum f(x) = ax² + bx + c, di mana a, b, dan c adalah konstanta. Grafik fungsi kuadrat adalah parabola. Parabola dapat terbuka ke atas atau ke bawah, tergantung pada nilai a. Jika a positif, parabola terbuka ke atas; jika a negatif, parabola terbuka ke bawah.
Contoh: f(x) = x² – 2x + 1
Grafik fungsi ini merupakan parabola yang terbuka ke atas. Titik puncak parabola dapat dihitung menggunakan rumus x = -b/2a. Untuk contoh ini, titik puncaknya adalah x = -(-2)/(2*1) = 1. Dengan mensubstitusikan x = 1 ke dalam fungsi, kita mendapatkan y = 1²
-2(1) + 1 = 0 . Jadi, titik puncaknya adalah (1, 0).
Titik potong sumbu-x terjadi ketika y = 0, dan dalam kasus ini, persamaan x²
-2x + 1 = 0 memiliki solusi tunggal x = 1. Grafiknya simetris terhadap garis tegak lurus sumbu-x yang melalui titik puncak.
Jenis-Jenis Grafik

Pemahaman terhadap berbagai jenis grafik sangat penting dalam matematika. Masing-masing jenis grafik memiliki karakteristik dan kegunaan yang berbeda-beda, sehingga penting untuk dapat membedakan dan memanfaatkannya dengan tepat.
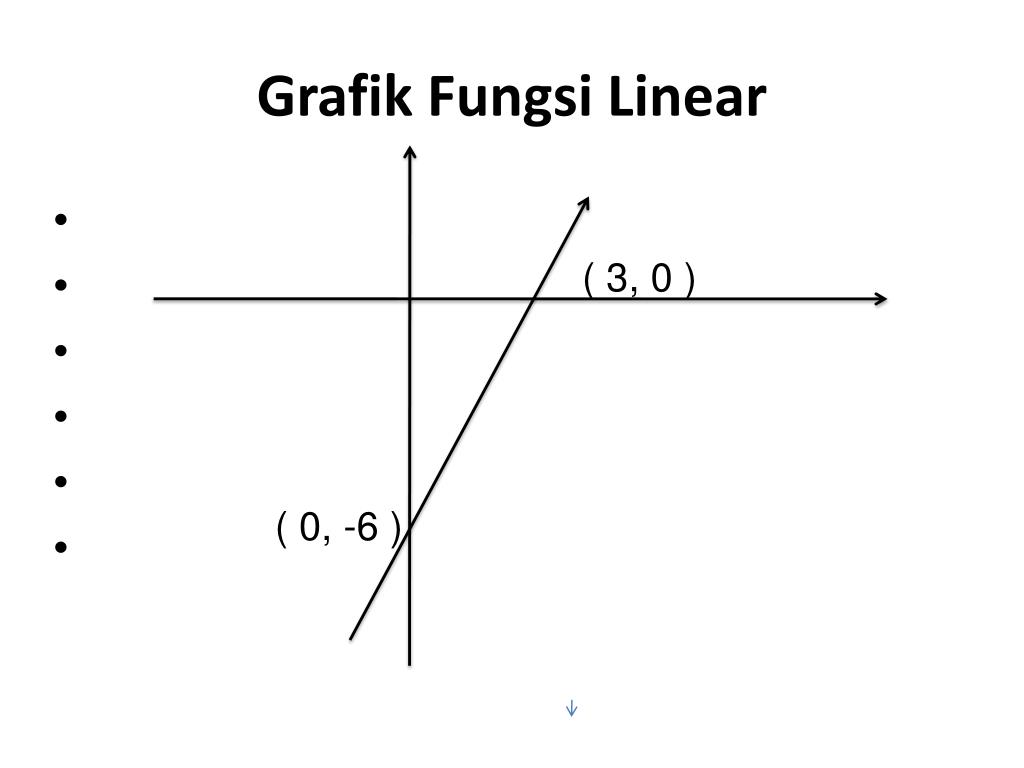
Grafik Fungsi Linear
Grafik fungsi linear merupakan representasi visual dari hubungan linier antara dua variabel. Bentuk umumnya adalah y = mx + c, di mana m adalah gradien dan c adalah titik potong sumbu-y. Grafik ini ditampilkan sebagai garis lurus.
- Karakteristik: Garis lurus, memiliki gradien konstan, setiap perubahan nilai x akan menghasilkan perubahan nilai y dengan rasio yang tetap.
- Kegunaan: Memudahkan visualisasi hubungan linier, menentukan titik potong, dan memprediksi nilai variabel lainnya.
Grafik Fungsi Kuadrat
Grafik fungsi kuadrat menggambarkan hubungan kuadratik antara dua variabel. Bentuk umumnya adalah y = ax 2 + bx + c, di mana a, b, dan c adalah konstanta. Grafik ini berbentuk parabola.
- Karakteristik: Bentuk parabola, memiliki titik puncak, dan simetris terhadap sumbu simetri.
- Kegunaan: Menentukan nilai maksimum atau minimum, menganalisis perilaku perubahan, dan memecahkan masalah optimasi.
Grafik Fungsi Eksponensial
Grafik fungsi eksponensial menggambarkan pertumbuhan atau penurunan eksponensial suatu variabel terhadap variabel lainnya. Bentuk umumnya adalah y = ab x, di mana a dan b adalah konstanta.
- Karakteristik: Memiliki satu titik potong sumbu-y, bentuknya meningkat atau menurun secara eksponensial.
- Kegunaan: Memahami pertumbuhan penduduk, peluruhan radioaktif, bunga majemuk, dan fenomena lainnya yang mengikuti pola eksponensial.
Grafik Trigonometri
Grafik trigonometri menggambarkan hubungan antara sudut dan nilai fungsi trigonometri seperti sinus, kosinus, dan tangen.
- Karakteristik: Grafik berulang secara periodik, memiliki amplitudo dan periode tertentu.
- Kegunaan: Mendeskripsikan gelombang, gerak harmonik sederhana, dan fenomena berulang lainnya.
Grafik Bar
Grafik bar digunakan untuk membandingkan nilai kategori-kategori tertentu. Setiap kategori diwakili oleh sebuah batang.
- Karakteristik: Membandingkan nilai kategori dengan tinggi batang, mudah dipahami.
- Kegunaan: Memvisualisasikan data diskrit, menampilkan perbandingan antara berbagai kategori.
Grafik Lingkaran (Pie Chart), Materi matematika grafik
Grafik lingkaran digunakan untuk menampilkan proporsi atau persentase dari suatu keseluruhan.
- Karakteristik: Memvisualisasikan proporsi dengan potongan-potongan lingkaran, mudah untuk melihat perbandingan.
- Kegunaan: Memperlihatkan proporsi berbagai bagian dari suatu keseluruhan.
Grafik Titik-Titik (Scatter Plot)
Grafik titik-titik digunakan untuk menunjukkan hubungan antara dua variabel numerik.
- Karakteristik: Titik-titik diplot berdasarkan koordinat variabel-variabel, menunjukkan pola korelasi.
- Kegunaan: Menentukan korelasi antara variabel, menemukan pola tren, dan memprediksi nilai satu variabel berdasarkan variabel lainnya.
Membuat Grafik Fungsi Linear
Berikut langkah-langkah membuat grafik fungsi linear y = 2x + 1:
- Pilih beberapa nilai x (misalnya, -2, -1, 0, 1, 2).
- Hitung nilai y yang sesuai untuk setiap nilai x menggunakan persamaan y = 2x + 1.
- Buat tabel dengan kolom x dan y.
- Plot titik-titik (x, y) pada bidang koordinat.
- Hubungkan titik-titik tersebut dengan garis lurus.
Konsep dan Prinsip Dasar
Memahami konsep koordinat Kartesius dan prinsip dasar dalam menggambar grafik sangat penting untuk mempelajari matematika. Pemahaman ini menjadi fondasi untuk menganalisis dan memahami hubungan antara variabel dalam berbagai fenomena.
Koordinat Kartesius dalam Grafik
Sistem koordinat Kartesius menggunakan dua garis bilangan yang saling tegak lurus, sumbu x dan sumbu y, untuk menentukan posisi titik pada bidang datar. Titik potong kedua sumbu tersebut adalah titik asal (0,0). Setiap titik pada bidang memiliki pasangan koordinat (x, y), di mana x adalah jarak titik tersebut dari sumbu y dan y adalah jarak titik tersebut dari sumbu x.
Hal ini memungkinkan kita untuk merepresentasikan data dan hubungannya secara visual.
Menentukan Titik Potong Sumbu
Titik potong sumbu x dan sumbu y pada sebuah grafik sangat penting untuk memahami karakteristik grafik. Titik potong sumbu x didapatkan dengan mensubstitusikan y = 0 ke dalam persamaan, sedangkan titik potong sumbu y didapatkan dengan mensubstitusikan x = 0.
- Titik Potong Sumbu X: Untuk menemukan titik potong sumbu x, kita perlu mencari nilai x ketika y = 0. Contohnya, pada persamaan y = 2x – 4, jika y = 0, maka 0 = 2x – 4. Dengan menyelesaikan persamaan tersebut, kita mendapatkan x = 2. Jadi, titik potong sumbu x adalah (2, 0).
- Titik Potong Sumbu Y: Untuk menemukan titik potong sumbu y, kita perlu mencari nilai y ketika x = 0. Contohnya, pada persamaan yang sama (y = 2x – 4), jika x = 0, maka y = 2(0)
-4. Dengan menyelesaikan persamaan tersebut, kita mendapatkan y = -4. Jadi, titik potong sumbu y adalah (0, -4).
Contoh Penerapan
Berikut contoh penerapan dalam menggambar grafik persamaan y = x 2
-3x + 2.
- Titik potong sumbu x: Jika y = 0, maka x 23x + 2 = 0. Persamaan ini dapat difaktorkan menjadi (x – 1)(x – 2) = 0. Ini menghasilkan titik potong sumbu x pada x = 1 dan x = 2, yaitu (1, 0) dan (2, 0).
- Titik potong sumbu y: Jika x = 0, maka y = 0 23(0) + 2 = 2. Ini menghasilkan titik potong sumbu y pada y = 2, yaitu (0, 2).
- Titik tambahan: Untuk menggambar grafik dengan lebih akurat, kita dapat mencari titik-titik lain pada grafik dengan memasukkan nilai x yang berbeda ke dalam persamaan. Misalnya, jika x = 3, maka y = 3 23(3) + 2 = 4. Titik (3, 4) juga berada pada grafik.
Langkah-Langkah Menggambar Grafik
- Tentukan persamaan grafik yang akan digambar.
- Tentukan titik potong sumbu x dan sumbu y.
- Tentukan beberapa titik tambahan pada grafik dengan memasukkan nilai x yang berbeda ke dalam persamaan.
- Plot titik-titik tersebut pada bidang koordinat Kartesius.
- Hubungkan titik-titik tersebut dengan garis atau kurva yang sesuai dengan bentuk grafik persamaan tersebut.
Hubungan Persamaan dan Grafik
Setiap persamaan memiliki representasi grafis pada bidang koordinat Kartesius. Bentuk grafik menggambarkan hubungan antara variabel-variabel dalam persamaan. Misalnya, grafik linier menunjukkan hubungan linier antara variabel, sedangkan grafik parabola menunjukkan hubungan kuadrat. Memahami hubungan ini memungkinkan kita untuk menganalisis dan menginterpretasikan informasi yang terkandung dalam persamaan.
Penerapan Materi Matematika Grafik
Grafik bukan hanya sekumpulan titik dan garis di atas kertas. Grafik memiliki peran penting dalam berbagai aspek kehidupan, dari perencanaan keuangan hingga analisis data ilmiah. Pemahaman tentang grafik memungkinkan kita untuk melihat tren, pola, dan hubungan dalam data, yang sangat bermanfaat untuk pengambilan keputusan.
Penerapan dalam Kehidupan Sehari-hari
Grafik dapat membantu kita memahami informasi dengan lebih mudah. Misalnya, grafik dapat digunakan untuk melacak pengeluaran bulanan, memantau pertumbuhan tanaman, atau menganalisis pola cuaca. Grafik membantu kita melihat tren dan pola dalam data yang mungkin tidak terlihat dengan mudah dalam bentuk angka-angka saja. Grafik membuat informasi lebih mudah dipahami dan diinterpretasikan.
Penerapan dalam Bidang Sains dan Teknik
Dalam sains dan teknik, grafik digunakan untuk merepresentasikan dan menganalisis data eksperimen. Grafik dapat menunjukkan hubungan antara variabel, seperti suhu dan tekanan, atau waktu dan kecepatan. Analisis grafik membantu peneliti dalam mengidentifikasi pola dan tren dalam data, yang dapat mengarah pada penemuan baru dan pemahaman yang lebih dalam tentang fenomena alam. Contohnya, grafik dapat digunakan untuk memodelkan pertumbuhan bakteri, mengidentifikasi efektivitas obat, atau menganalisis data seismograf.
Analisis Tren dan Pola Data
Grafik memungkinkan kita untuk mengidentifikasi tren dan pola dalam data dengan cepat. Misalnya, grafik dapat menunjukkan peningkatan penjualan produk tertentu dari waktu ke waktu, atau penurunan populasi spesies tertentu. Tren dan pola ini dapat digunakan untuk memprediksi kejadian di masa depan, membuat keputusan bisnis, atau mengidentifikasi potensi masalah.
Pemecahan Masalah Dunia Nyata
Grafik digunakan untuk memecahkan masalah dunia nyata dalam berbagai bidang. Misalnya, dalam bidang transportasi, grafik dapat digunakan untuk mengoptimalkan jalur pengiriman barang. Dalam bidang kesehatan, grafik dapat digunakan untuk melacak kemajuan pasien. Dalam bidang ekonomi, grafik dapat digunakan untuk menganalisis tren pasar dan memprediksi fluktuasi harga. Grafik memungkinkan solusi yang lebih terarah dan terukur untuk berbagai permasalahan.
Penerapan dalam Bidang Ekonomi (Grafik Permintaan dan Penawaran)
- Grafik permintaan menunjukkan hubungan antara harga suatu barang dan jumlah barang yang diminta oleh konsumen pada tingkat harga tertentu. Grafik ini biasanya berupa kurva yang menurun dari kiri atas ke kanan bawah.
- Grafik penawaran menunjukkan hubungan antara harga suatu barang dan jumlah barang yang ditawarkan oleh produsen pada tingkat harga tertentu. Grafik ini biasanya berupa kurva yang meningkat dari kiri bawah ke kanan atas.
- Perpotongan antara kurva permintaan dan penawaran menunjukkan titik keseimbangan pasar, di mana jumlah barang yang diminta sama dengan jumlah barang yang ditawarkan. Titik keseimbangan ini menunjukkan harga dan kuantitas optimal di pasar.
Sebagai ilustrasi, bayangkan grafik permintaan dan penawaran untuk harga beras. Kurva permintaan akan menunjukkan bahwa semakin rendah harga beras, semakin banyak beras yang akan dibeli konsumen. Sebaliknya, kurva penawaran akan menunjukkan bahwa semakin tinggi harga beras, semakin banyak beras yang akan ditawarkan oleh petani. Perpotongan kedua kurva tersebut menunjukkan harga dan jumlah beras yang seimbang di pasar.
Representasi Visual
Dalam menganalisis data, visualisasi data menjadi kunci untuk memahami informasi dengan cepat dan mudah. Representasi visual yang tepat dapat memperjelas tren, pola, dan hubungan antar variabel. Berikut beberapa contoh visualisasi yang sering digunakan.
Contoh Grafik Bar untuk Perbandingan
Grafik bar digunakan untuk membandingkan nilai dari beberapa kategori. Misalnya, untuk membandingkan penjualan produk A, B, dan C pada kuartal pertama tahun 2024. Grafik bar akan menampilkan batang-batang dengan tinggi yang berbeda, yang merepresentasikan nilai penjualan masing-masing produk. Semakin tinggi batang, semakin besar penjualannya.
Berikut contoh sederhana:
| Produk | Penjualan (dalam ribuan rupiah) |
|---|---|
| A | 150 |
| B | 200 |
| C | 100 |
Grafik bar akan menampilkan batang untuk produk A setinggi 150, produk B setinggi 200, dan produk C setinggi 100.
Contoh Grafik Lingkaran untuk Proporsi
Grafik lingkaran, atau pie chart, efektif untuk menunjukkan proporsi atau persentase dari suatu keseluruhan. Misalnya, untuk menunjukkan proporsi pembagian pendapatan suatu perusahaan dari berbagai divisi. Setiap potongan lingkaran mewakili persentase pendapatan dari divisi tersebut.
Contoh: Jika divisi pemasaran mendapatkan 30% dari pendapatan, maka potongan lingkaran yang mewakili divisi pemasaran akan berukuran 30% dari lingkaran keseluruhan.
Contoh Grafik Garis untuk Tren Perubahan
Grafik garis digunakan untuk menampilkan tren atau perubahan data dari waktu ke waktu. Misalnya, untuk menunjukkan pertumbuhan jumlah pengguna suatu aplikasi selama beberapa bulan. Grafik akan menampilkan garis yang menghubungkan titik-titik data, sehingga tren perubahan data terlihat jelas.
Contoh: Titik data pada bulan Januari 2024 menunjukkan jumlah pengguna 1000, dan titik data pada bulan Februari 2024 menunjukkan jumlah pengguna 1200. Garis yang menghubungkan kedua titik tersebut menunjukkan peningkatan jumlah pengguna.
Memilih Jenis Grafik yang Tepat
Pemilihan jenis grafik yang tepat bergantung pada jenis data yang ingin divisualisasikan. Grafik bar cocok untuk membandingkan nilai kategori. Grafik lingkaran ideal untuk menampilkan proporsi. Grafik garis cocok untuk menampilkan tren perubahan dari waktu ke waktu. Penting untuk memilih jenis grafik yang paling efektif untuk menyampaikan informasi secara akurat dan mudah dipahami.
- Jika ingin membandingkan nilai dari beberapa kategori, gunakan grafik bar.
- Jika ingin menunjukkan proporsi dari keseluruhan, gunakan grafik lingkaran.
- Jika ingin menampilkan tren perubahan data dari waktu ke waktu, gunakan grafik garis.
Informasi Penting dalam Grafik
Grafik yang efektif harus menampilkan informasi penting secara jelas. Informasi tersebut meliputi judul grafik, label sumbu (jika ada), keterangan, dan legenda. Juga penting untuk memilih skala yang tepat pada sumbu agar informasi yang disajikan akurat dan tidak menyesatkan. Hindari penggunaan warna yang terlalu banyak atau tidak sesuai, agar grafik tetap mudah dibaca.
Soal dan Latihan
Berikut ini disajikan beberapa soal dan latihan untuk mengasah pemahaman Anda tentang materi matematika grafik. Soal-soal ini dirancang untuk membantu Anda mempraktikkan konsep-konsep yang telah dipelajari sebelumnya. Latihan-latihan ini meliputi soal pilihan ganda, soal uraian, dan contoh aplikasi dalam kehidupan sehari-hari.
Soal Pilihan Ganda
Berikut ini tiga soal pilihan ganda untuk menguji pemahaman Anda tentang grafik.
- Grafik fungsi y = 2 x + 1 akan melalui titik …
- A. (1, 3)
- B. (0, 1)
- C. (2, 5)
- D. Semua pilihan benar
- Grafik fungsi y = – x2 + 4 akan memotong sumbu- y pada titik …
- A. (0, 4)
- B. (4, 0)
- C. (0, -4)
- D. (-4, 0)
- Grafik fungsi y = 1/2 x
3 memiliki gradien (kemiringan) sebesar …
- A. 1/2
- B. -3
- C. 3
- D. -1/2
Jawaban: D. Semua pilihan benar. Ketiga titik tersebut memenuhi persamaan y = 2 x + 1.
Jawaban: A. (0, 4). Substitusikan x = 0 ke dalam persamaan.
Jawaban: A. 1/2. Gradien suatu persamaan dalam bentuk y = mx + c adalah m.
Soal Uraian
Berikut ini lima soal uraian yang mengharuskan Anda menjelaskan langkah-langkah menggambar grafik.
- Gambarkan grafik fungsi y = x2 – 2 x + 1.
- Gambarkan grafik fungsi y = 2 x.
- Gambarkan grafik fungsi y = | x + 3|.
- Gambarkan grafik persamaan 3 x + 2 y = 6.
- Gambarkan grafik fungsi y = sin( x).
Petunjuk: Untuk soal-soal uraian, langkah-langkahnya meliputi menentukan titik potong sumbu- x dan sumbu- y, mencari titik-titik tambahan, dan menghubungkan titik-titik tersebut untuk membentuk grafik.
Contoh Aplikasi Grafik dalam Kehidupan Sehari-hari
Grafik dapat digunakan untuk merepresentasikan berbagai fenomena dalam kehidupan sehari-hari. Misalnya, grafik dapat digunakan untuk menggambarkan pertumbuhan penduduk suatu kota dari waktu ke waktu atau untuk menunjukkan pola konsumsi energi suatu rumah tangga.
Contoh lainnya adalah dalam bidang ekonomi, grafik dapat digunakan untuk menganalisis tren harga saham, atau untuk memperlihatkan perbandingan penjualan produk A dan B.
Kunci Jawaban Soal Uraian
Kunci jawaban untuk soal uraian di atas akan diberikan secara terpisah. Penjelasan langkah demi langkah untuk menggambar grafik akan disertakan.
Kesimpulan
Dengan memahami materi matematika grafik, kita dapat mengolah dan menganalisis data dengan lebih efektif. Grafik bukan hanya alat visualisasi, tetapi juga alat analisis yang ampuh untuk menemukan insight dan memecahkan masalah. Semoga materi ini memberikan pemahaman yang komprehensif dan mendalam tentang visualisasi data menggunakan grafik.